Dijkstra's Algorithm

1. What is Dijkstra's Algorithm?

Dijkstra's Algorithm is a famous algorithm used for finding the shortest paths between nodes in a graph. It is widely used in routing and navigation systems. The algorithm works on both directed and undirected graphs with non-negative edge weights.

Dijkstra’s algorithm is a popular algorithms for solving many single-source shortest path problems having non-negative edge weight in the graphs i.e., it is to find the shortest distance between two vertices on a graph. It was conceived by Dutch computer scientist Edsger W. Dijkstra in 1956.

2. Algorithm for Dijkstra's Algorithm

1. Initialize the distance to the start node as 0 and to all other nodes as infinity.
2. Push the start node into a priority queue (min-heap) with distance 0.
3. While the priority queue is not empty:
   • Pop the node with the smallest distance from the queue.
   • For each adjacent node, calculate the distance to it through the current node.
   • If this distance is less than the known distance, update the shortest distance and push the node into the queue.
4. Continue the process until all nodes have been processed.

3. How Does Dijkstra's Algorithm Work?

1. Start with the initial node, setting its distance to 0 and all others to infinity.
2. Use a priority queue to explore the nearest unvisited node.
3. Update the distances to all adjacent nodes, pushing nodes with updated distances into the queue.
4. Repeat until all nodes are processed, ensuring the shortest paths from the start node to all other nodes.

Consider the below graph:

Step 1: Start from Node 0 and mark Node as visited as you can check in below image visited Node is marked red.

Step 2: Check for adjacent Nodes, Now we have to choices (Either choose Node1 with distance 2 or either choose Node 2 with distance 6 ) and choose Node with minimum distance. In this step Node 1 is Minimum distance adjacent Node, so marked it as visited and add up the distance.

Distance: Node 0 -> Node 1 = 2

Step 3: Then Move Forward and check for adjacent Node which is Node 3, so marked it as visited and add up the distance, Now the distance will be:

Distance: Node 0 -> Node 1 -> Node 3 = 2 + 5 = 7

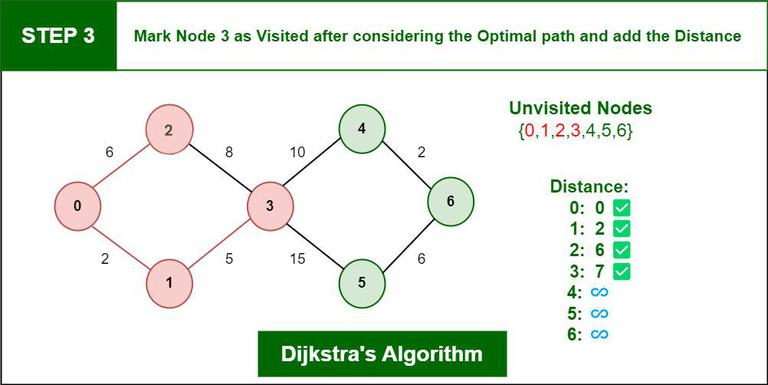
Step 4: Again we have two choices for adjacent Nodes (Either we can choose Node 4 with distance 10 or either we can choose Node 5 with distance 15) so choose Node with minimum distance. In this step Node 4 is Minimum distance adjacent Node, so marked it as visited and add up the distance.

Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 = 2 + 5 + 10 = 17

Step 5: Again, Move Forward and check for adjacent Node which is Node 6, so marked it as visited and add up the distance, Now the distance will be:

Distance: Node 0 -> Node 1 -> Node 3 -> Node 4 -> Node 6 = 2 + 5 + 10 + 2 = 19 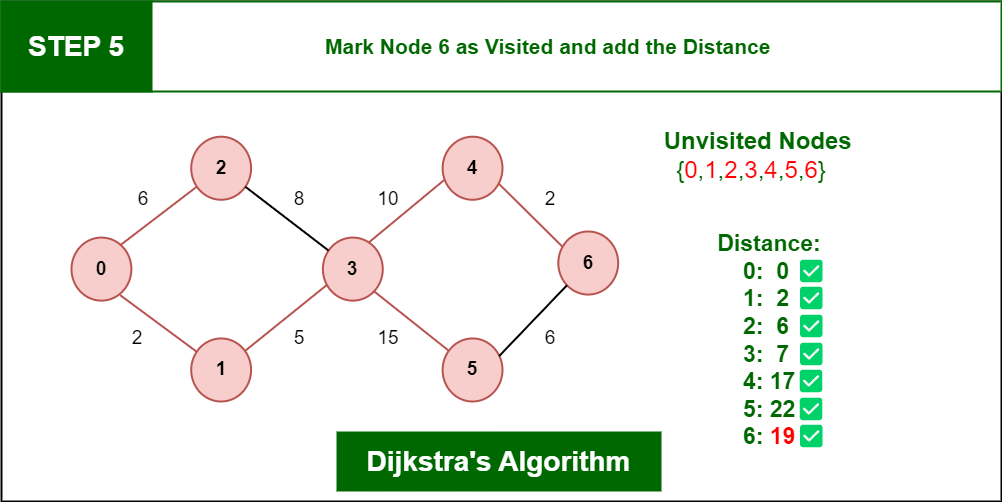So, the Shortest Distance from the Source Vertex is 19 which is optimal one

4. Problem Description

Given a graph with vertices and weighted edges, find the shortest path from a starting vertex to all other vertices.

5. Examples

Example 1:

Input:
Graph: {A: [(B, 1), (C, 4)], B: [(A, 1), (C, 2), (D, 5)], C: [(A, 4), (B, 2), (D, 1)], D: [(B, 5), (C, 1)]}
Start node: A

Output:
Shortest distances: {A: 0, B: 1, C: 3, D: 4}

Example 2:

Input:
Graph: {1: [(2, 2), (3, 4)], 2: [(1, 2), (3, 1)], 3: [(1, 4), (2, 1)]}
Start node: 1

Output:
Shortest distances: {1: 0, 2: 2, 3: 3}

6. Constraints

• The graph must have non-negative edge weights.
• The graph can be directed or undirected.

7. Implementation

Python

import heapq

def dijkstra(graph, start):
    pq = [(0, start)]
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0

    while pq:
        current_distance, current_vertex = heapq.heappop(pq)

        if current_distance > distances[current_vertex]:
            continue

        for neighbor, weight in graph[current_vertex]:
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor))

    return distances

C++

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <set>
using namespace std;

typedef pair<int, int> pii;

unordered_map<int, int> dijkstra(unordered_map<int, vector<pii>>& graph, int start) {
    priority_queue<pii, vector<pii>, greater<pii>> pq;
    unordered_map<int, int> distances;

    for (auto& node : graph) {
        distances[node.first] = INT_MAX;
    }

    distances[start] = 0;
    pq.push({0, start});

    while (!pq.empty()) {
        int current_distance = pq.top().first;
        int current_vertex = pq.top().second;
        pq.pop();

        if (current_distance > distances[current_vertex]) continue;

        for (auto& neighbor : graph[current_vertex]) {
            int weight = neighbor.second;
            int next_vertex = neighbor.first;
            int distance = current_distance + weight;

            if (distance < distances[next_vertex]) {
                distances[next_vertex] = distance;
                pq.push({distance, next_vertex});
            }
        }
    }

    return distances;
}

void shortDijkstra(int src, int n, vector<vector<pii>>& adjList) {
    vector<int> dist(n, INT_MAX);
    set<pii> st;
    
    dist[src] = 0;
    st.insert({0, src});
    
    while (!st.empty()) {
        auto mini = *st.begin();
        
        int nodedistance = mini.first;
        int node = mini.second;
        
        st.erase(st.begin());
        
        for (auto nbr : adjList[node]) {
            int dis = nodedistance + nbr.second;
            if (dis < dist[nbr.first]) {
                auto result = st.find(make_pair(dist[nbr.first], nbr.first));
                if (result != st.end()) {
                    st.erase(result);
                }
                dist[nbr.first] = dis;
                st.insert(make_pair(dist[nbr.first], nbr.first));
            }
        }
    }
    cout << "Printing ans" << endl;
    for (auto i : dist) {
        cout << i << " ";
    }
}

Java

import java.util.*;

class Graph {
    private Map<Integer, List<int[]>> graph = new HashMap<>();

    public void addEdge(int source, int destination, int weight) {
        graph.computeIfAbsent(source, k -> new ArrayList<>()).add(new int[]{destination, weight});
        graph.computeIfAbsent(destination, k -> new ArrayList<>()).add(new int[]{source, weight});
    }

    public Map<Integer, Integer> dijkstra(int start) {
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
        Map<Integer, Integer> distances = new HashMap<>();
        for (int node : graph.keySet()) distances.put(node, Integer.MAX_VALUE);

        distances.put(start, 0);
        pq.add(new int[]{start, 0});

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int currentNode = current[0];
            int currentDistance = current[1];

            if (currentDistance > distances.get(currentNode)) continue;

            for (int[] neighbor : graph.get(currentNode)) {
                int nextNode = neighbor[0];
                int weight = neighbor[1];
                int distance = currentDistance + weight;

                if (distance < distances.get(nextNode)) {
                    distances.put(nextNode, distance);
                    pq.add(new int[]{nextNode, distance});
                }
            }
        }

        return distances;
    }
}

JavaScript

class PriorityQueue {
    constructor() {
        this.values = [];
    }
    enqueue(val, priority) {
        this.values.push({val, priority});
        this.sort();
    }
    dequeue() {
        return this.values.shift();
    }
    sort() {
        this.values.sort((a, b) => a.priority - b.priority);
    }
}

function dijkstra(graph, start) {
    const pq = new PriorityQueue();
    const distances = {};
    for (let vertex in graph) {
        distances[vertex] = Infinity;
    }
    distances[start] = 0;
    pq.enqueue(start, 0);

    while (pq.values.length) {
        let {val: currentVertex, priority: currentDistance} = pq.dequeue();

        if (currentDistance > distances[currentVertex]) continue;

        for (let [neighbor, weight] of graph[currentVertex]) {
            let distance = currentDistance + weight;

            if (distance < distances[neighbor]) {
                distances[neighbor] = distance;
                pq.enqueue(neighbor, distance);
            }
        }
    }

    return distances;
}

8. Complexity Analysis

• Time Complexity: $O(E log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This is due to the priority queue operations.
• Space Complexity: $O(V)$, for storing distances and the priority queue.

9. Advantages and Disadvantages

Advantages:

• Efficient for graphs with non-negative weights.
• Provides the shortest path from a single source to all other vertices.

Disadvantages:

• Cannot handle graphs with negative weight edges.
• More complex to implement compared to simpler algorithms like BFS for unweighted graphs.

10. Resources

• GFG Problem: GFG Problem
• HackerRank Problem: HackerRank
• Author's Geeks for Geeks Profile: MuraliDharan
• Video Explanation:
  • Dijkstra's Algorithm | GeeksforGeeks
  • Shortest Path Algorithms | Computer Science